Kapitel 4 Strukturierte Datentypen

Basierend auf den einfachen (atomaren) Datentypen existieren in R die folgenden grundlegenden Datenstrukturen.

Datenstruktur Beschreibung
vector Sequenz gleicher Datentypen
matrix Verallg. Vektor in 2 Dimensionen
array Verallg. Vektor mit beliebigen Dimensionen
list Sequenz ungleicher Datentypen
data frame Spezielle Liste mit Vektoren gleicher Länge

Schema:

Dimension Homogen Heterogen
1-Dim. vector list
2-Dim. matrix data frame
k-Dim. array

Vektoren und Matrizen sind eine strukturierte Zusammenstellung von Daten gleichen Typs. Ein Vektor kann zum Beispiele eine Reihe von integer Werten bündeln, dann aber keine zusätzlichen logischen Werte oder Zeichenketten aufnehmen. Im Gegensatz dazu erlauben es uns Listen und Data Frames, auch Daten unterschiedlichen Typs zu bündeln. In diesem Kapitel wollen wir uns damit beschäftigen, welche Implikationen die hier skizzierten Eigenschaften der verschiedenen Datenstrukturen für Ihre Anwendung haben.

Damit die Datenstruktur für euch auch visuell an Gestalt gewinnt, folgt eine vereinfachte Darstellung mit den zentralen Eigenschaften der Datenstrukturen. Die Darstellung ist nicht in jeder Hinsicht korrekt, soll aber dazu dienen, die grundlegenden Unterschiede der verschiedenen Datenstrukturen zu veranschaulichen.

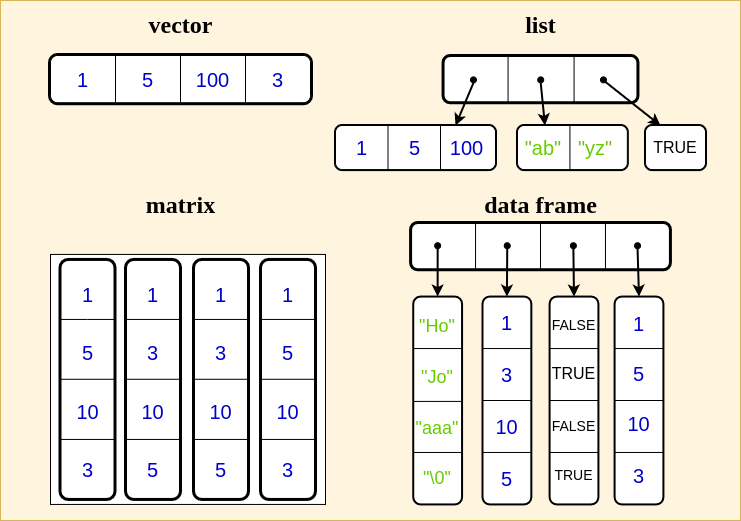
Strukturierte Datentypen

Abb. 4.1: Strukturierte Datentypen

4.1 Vektoren

Vektoren sind sequentiell geordnete Folgen von Werten gleichen Typs. Sie können auf ganz unterschiedliche Art erzeugt werden.

Beispiel: Informationen zum Lineup für die Clubnacht heute. Mit der Funktion c() (kurz für ‘concatenate’ / ‘combine’).

DJ_Alter <- c(34, 38, 28, 25, 20)
DJ_Name <- c("DJ Puma", "Cabanne", "Molly", "Echoton", "cv313")
DJ_Vinyl <- c(FALSE, TRUE ,TRUE ,FALSE , FALSE)

DJ_Alter
## [1] 34 38 28 25 20
DJ_Name
## [1] "DJ Puma" "Cabanne" "Molly"   "Echoton" "cv313"
DJ_Vinyl
## [1] FALSE  TRUE  TRUE FALSE FALSE

Anmerkung: Die DJs gibt es wirklich und es lohnt sich mal reinzuhören :). Das Alter und ob die Personen mit Vinyl auflegen oder nicht, ist allerdings frei erfunden.

Ganz einfach können wir Vektoren auch mit dem Colon-Operator : erzeugen, welcher Zahlenfolgen mit Inkrement 1/-1 generiert.

1:4
## [1] 1 2 3 4
countdown <- 10:0
countdown
##  [1] 10  9  8  7  6  5  4  3  2  1  0
-1.2:5
## [1] -1.2 -0.2  0.8  1.8  2.8  3.8  4.8

Allgemeinere Folgen können auch mit seq() erzeugt werden:

seq(from = 1,
    to = 3,
    by = 0.5)
## [1] 1.0 1.5 2.0 2.5 3.0

Auch sehr nützlich:

rep(x = c("Nein!","Doch!"),
    times = 3)
## [1] "Nein!" "Doch!" "Nein!" "Doch!" "Nein!" "Doch!"

4.1.1 Abfragen von Werten durch Subsetting von Vektoren

Mit dem [] Operator können einzelne Elemente eines Vektors abgefragt werden. Hier zum Beispiel die Indexposition 2:

DJ_Alter[2]
## [1] 38

Der Operator ist aber tatsächlich ein “Subset”-Operator und damit wesentlich flexibler und sehr mächtig:

DJ_Name[c(1, 3)]
## [1] "DJ Puma" "Molly"
DJ_Name[-c(1, 3)]
## [1] "Cabanne" "Echoton" "cv313"

Der Subset-Operator ermöglicht es uns also auch eine Teilmenge des Vektors nach bestimmten Kriterien abzufragen. Hier zum Beispiel die Teilmenge derjenigen Werte, die einen entsprechenden Index haben. Man kann [] als einen Operator verstehen, welcher von links auf ein Vektorobjekt angewendet wird.

Wird anstelle eines Index ein logischer Vektor (geeigneter Länge) übergeben, so werden alle zugehörigen “wahren” Elemente des Vektors zurückgegeben.

Dies ist tatsächlich eine der häufigsten Verwendungen des Operators (bzw. der Funktion):

DJ_Name
## [1] "DJ Puma" "Cabanne" "Molly"   "Echoton" "cv313"
DJ_Vinyl
## [1] FALSE  TRUE  TRUE FALSE FALSE
DJ_Name[DJ_Vinyl]
## [1] "Cabanne" "Molly"

4.1.2 Vektorisierte Operationen

Alle atomaren Datentypen sind tatsächlich Vektoren der Länge eins

zahl <- 1
p <- TRUE
name <- "Tom"
  
length(zahl)
## [1] 1
length(p)
## [1] 1
length(name)
## [1] 1

Dadurch ist es moglich (fast) alle Operationen, welche für atomare Datentypen definiert sind vektorisierte anzuwenden, d.h. elementweise für ganze Vektoren:

x <- c(1,2,3)
y <- c(2,1,3)

x + y
## [1] 3 3 6
x + 1
## [1] 2 3 4
log(x)
## [1] 0.0000000 0.6931472 1.0986123
DJ_Alter > 21
## [1]  TRUE  TRUE  TRUE  TRUE FALSE

Der letzte Ausdruck wertet elementweise aus, ob das jeweilige Alter größer als 21 ist und bildet das Ergebnis in einem logischen Vektor entsprechender Länge ab.

Zur Illustration der folgenden Beispiele benötigen wir noch einen weiteren numerischen Vektor. Da wir nun wissen, wie man vektorisierte Operationen durchführt, können wir leicht einen Vektor mit den ungefähren Geburtsjahren der Personen aus deren Alter berechnen:

DJ_Geburtsjahr <- 2022 - DJ_Alter
DJ_Geburtsjahr
## [1] 1988 1984 1994 1997 2002

4.1.3 Operationen auf Vektoren

Abhängig vom Datentyp eines Vektors existieren verschiedene Funktionen, die einen Vektor als Argument nehmen und diesen auf ein Ergebnis abbilden.

Operation Beschreibung
length() Länge eines Vektors
mean() Durchschnittswert eines num. Vektors
max() Maximum eines num. Vektors
any() Ist irgendein Wert eines log. Vektors wahr? 
mean(DJ_Alter) # numerischer Vektor
## [1] 29
any(DJ_Vinyl) # logischer Vektor
## [1] TRUE

4.2 Faktoren: ein spezieller Datentyp für kategoriale Daten

Die Klasse factor ist in R ein eigener Datentyp, welcher die Typen integer und character derart verbindet, dass man geeignet kategoriale Variablen (nominal/ordinales Messniveau) repräsentieren kann. Dieser Datentyp ist eine Besonderheit von R und ermöglicht es, einfacher kategoriale Variablen statistisch zu untersuchen.
Mit der Funktion factor() können wir einem Vektor die Menge der möglichen Ausprägungen (levels) und deren Bezeichnungen (labels) zuordnen.

x <- factor(x = c(0, 1, 0, 1),                  # Vektor 
            levels = c(0, 1, 2),                # Mögliche Werte
            labels = c("Mann","Frau","Divers")) # Bezeichnungen 
x
## [1] Mann Frau Mann Frau
## Levels: Mann Frau Divers

Die Werte, die in einem Faktor vorkommen können, werden als level bezeichnet und können über die Funktion levels() abgerufen werden. Es spielt hierbei keine Rolle, ob die Werte tatsächlich in dem Vektor auftreten.

levels(x)
## [1] "Mann"   "Frau"   "Divers"

Die Level werden intern mit Integers repräsentiert. Die labels geben Namen für die entsprechenden Levels vor.

as.integer(x)
## [1] 1 2 1 2

Nicht nur character-Vektoren lassen sich in Faktoren umschreiben. Jeder homogene Daten-Vektor kann als Faktor geschrieben werden. Soll dabei auf Labels verzichtet werden, vereinfacht sich das Erstellen:

grades <- as.factor(x = 1:6)

grades
## [1] 1 2 3 4 5 6
## Levels: 1 2 3 4 5 6

Faktoren sind insbesondere hilfreich für deskriptive Statistiken und Abbildungen, da sie es ermöglichen, auch mögliche Ausprägungen eines Merkmals darzustellen, die im Datensatz nicht vorkommen.

Beispielsweise wurde der Wohnort von Studierenden in Leipzig mit den möglichen Antworten Zentrum, Nord, Süd, Ost und West abgefragt. Der character-Vektor z beinhaltet die Antworten einiger Studierender.

z <- c("Nord", "Ost", "Ost", "West", "Süd", "Nord", "Ost")
z
## [1] "Nord"       "Ost"        "Ost"        "West"       "S<U+00FC>d"
## [6] "Nord"       "Ost"

Eine einfache Häufigkeitstabelle zeigt die absoluten Häufigkeiten der Antworten:

table(z)
## z
##       Nord        Ost S<U+00FC>d       West 
##          2          3          1          1

Wie wir sehen, hat keine der befragten Studierenden angegeben, im Leipziger Zentrum zu wohnen. Der Wert taucht in der Häufigkeitstabelle also auch nicht auf. Mithilfe eines Faktors können wir nun die Menge aller möglichen Ausprägungen hinterlegen und so auch die Ausprägung mit 0 Antworten sichtbar machen.

z <- factor(z,
            levels = c("Nord", "Süd", "Ost", "West", "Zentrum"))

table(z)
## z
##       Nord S<U+00FC>d        Ost       West    Zentrum 
##          2          1          3          1          0

Dies ist auch hinfreich für Abbildungen (siehe Abschnitt 9).

plot(z)

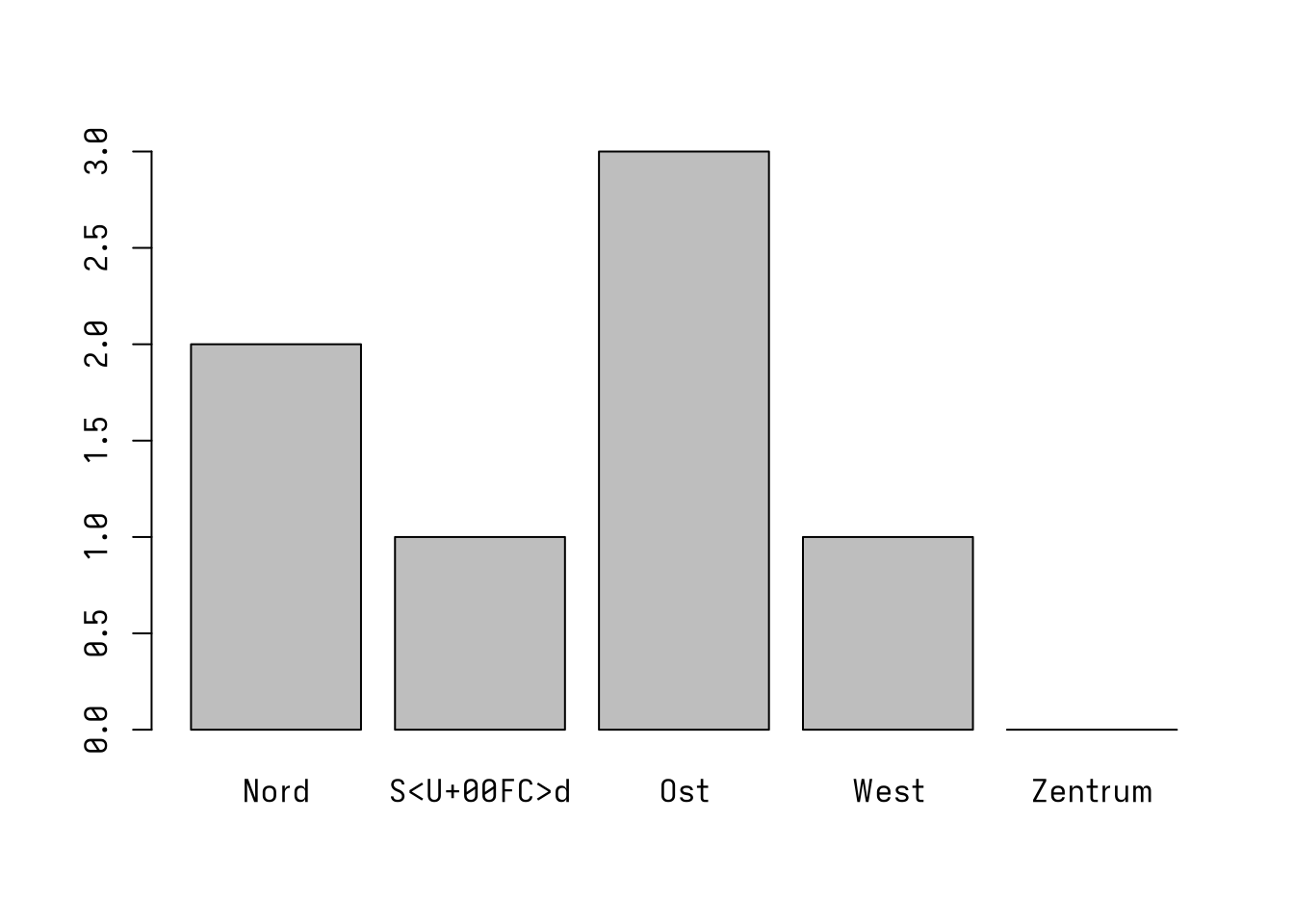
Für die Anordnung der Levels, das Umkodieren oder das Hinzufügen und Löschen einzelner Levels eignet sich das Paket forcats.

4.3 Matrizen

Die Datenstruktur einer Matrix verallgemeinert das Konzept des Vektors in zwei Dimensionen. Eine Matrix kann z.B. mittels eines Vektors mit der Funktion matrix() generiert werden:

M <- matrix(data = 1:9,
            nrow = 3,
            ncol = 3,
            byrow = TRUE)
M
##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

Die Rückgabe gibt uns schon einen Hinweis darauf, wie wir die Matrix “subsetten” können. In den eckigen Klammern ist jeweils der Index vermerkt, welche Zeile bzw. Spalte dargestellt wird.

Die Indizierung erfolgt dann ähnlich zu Vektoren:

M[1, 2]
## [1] 2

Lassen wir ein Argument offen und geben zum Beispiel nur einen Zeilenindex an, evaluiert der Ausdruck entsprechend zur gesamten angegebenen Zeile.

M[2, ]  
## [1] 4 5 6

Analog kann auch nur das Argument für die Spalte angeben werden:

M[, 1]
## [1] 1 4 7

4.3.1 Benennung von Spalten

Mit der Funktion colnames() lassen sich die Spalten (columns) einer Matrix benennen/ändern sowie auch abrufen.

colnames(M) <- c("A", "B", "C")
M
##      A B C
## [1,] 1 2 3
## [2,] 4 5 6
## [3,] 7 8 9
colnames(M)
## [1] "A" "B" "C"

Gleiches gilt für die Zeilen einer Matrix mit der Funktion rownames().

Über die Spaltennamen kann nun auch auf die Elemente der Matrix zugegriffen werden:

M[, "B"]
## [1] 2 5 8

4.3.2 Erzeugung von Matrizen aus Vektoren

Zwei Vektoren können mit der Funktion cbind() in eine Matrix überführt werden.

D <- cbind(DJ_Alter, DJ_Geburtsjahr)
D
##      DJ_Alter DJ_Geburtsjahr
## [1,]       34           1988
## [2,]       38           1984
## [3,]       28           1994
## [4,]       25           1997
## [5,]       20           2002

Analog können mit rbind() zwei Vektoren als Zeilen zu einer Matrix gebunden werden.

Achtung! Achtet darauf, dass die beiden Vektoren den gleichen atomaren Datentyp haben, andernfalls wird der “niedrigwertigere” der beiden zum Typ des “höherwertigen” konvertiert. Bindet man z.B. mit der Funktion cbind() einen Vektor vom Typ character und einen vom Typ logical, so erhält man eine Matrix mit ausschließlich Werten vom Typ character.

4.4 Listen

Eine Liste ist ein “verallgemeinerter Vektor” und lässt als Elemente beliebige Werte oder Datenstrukturen zu:

profil_marie <- list(Name    = "Marie", 
                     Freunde = c("Daphne", "Peer"),
                     Alter   = 24)
profil_marie
## $Name
## [1] "Marie"
## 
## $Freunde
## [1] "Daphne" "Peer"  
## 
## $Alter
## [1] 24

Die Elemente können gleich einen Namen zugeordnet werden.

4.4.1 Indizierung von Listen

Die Indizierung von Listen funktioniert etwas anders als bei den homogenen Datenstrukturen, da die Liste eigentlich nur Referenzen auf Objekte sammelt. Wenn wir die einzelnen Objekte für Operationen verwenden wollen, nutzen wir am besten den $ (Dollar)-Operator. Mit diesem können die Objekte, auf welche die Liste verweist, direkt “angesprochen” werden.

profil_marie$Name
## [1] "Marie"
profil_marie$Freunde
## [1] "Daphne" "Peer"

Die Verwendung des mittlerweile altbekannten Subset-Operators ist ebenfalls möglich. Allerdings muss hier immer die verschachtelte Struktur der Liste berücksichtigt werden, was es deutlich komplizierter macht.

Hier ein Beispiel:

profil_marie[2]
## $Freunde
## [1] "Daphne" "Peer"

Mit diesem Aufruf erhalten wir einen Verweis, welcher auf einen Vektor zeigt, welcher die Zeichenketten “Daphne” und “Peer” beinhaltet.

profil_marie[[2]][1]
## [1] "Daphne"

Diese Funktion bezieht sich im ersten Teil profil_marie[[2]] nun tatsächlich auf den Vektor, auf welchen die Referenz zeigt. Auf diesen wird anschließend nun noch einmal der Subset-Operator für die erste Position angewandt (Unser_Vektor[1]). Auf diese Weise erhalten wir das erste Element des Vektors (was wiederum ein einelementiger Vektor ist).

Deutlich einfacher ist hingegen die Indizierung mithilfe des Dollar-Operators und dem Objektnamen. Der Code wird dadurch wesentlich übersichtlicher:

profil_marie$Freunde[1]
## [1] "Daphne"

Falls ihr noch tiefer in das Subsetting von Listen einsteigen wollt, empfiehlt sich das Kapitel “Subsetting” aus dem Buch Advanced R.

4.5 Data Frames

Die für statistische Zwecke häufigste und wichtigste Datenstruktur ist die einer Datentabelle, ein sogenanntes dataframe.

Diese kann ganz einfach aus Vektoren erzeugt werden:

df_lineup <- data.frame(Name  = DJ_Name, 
                        Alter = DJ_Alter)
df_lineup
##      Name Alter
## 1 DJ Puma    34
## 2 Cabanne    38
## 3   Molly    28
## 4 Echoton    25
## 5   cv313    20

4.5.1 Indizierung von Datentabellen

Das Subsetting funktioniert hier wieder Analog zur Matrix:

df_lineup[3, ]
##    Name Alter
## 3 Molly    28
df_lineup[, 2]
## [1] 34 38 28 25 20

Wie bei den Listen ist es aber auch hier möglich, die Spalten über ihren Namen zu selektieren.

df_lineup$Name
## [1] "DJ Puma" "Cabanne" "Molly"   "Echoton" "cv313"

4.5.2 Aufnahme weiterer Variablen/Spalten

Wie bei den Matrizen auch, können mit der Funktion cbind() Vektoren als Spalten eines bereits bestehenden Data Frames aufgenommen werden.

Wie bei Matrizen können Vektoren mit der Funktion cbind() als Spalten in einen bestehenden Dataframe eingefügt werden.

df_lineup <- cbind(df_lineup, DJ_Vinyl)
df_lineup
##      Name Alter DJ_Vinyl
## 1 DJ Puma    34    FALSE
## 2 Cabanne    38     TRUE
## 3   Molly    28     TRUE
## 4 Echoton    25    FALSE
## 5   cv313    20    FALSE

Alternativ kann eine Spalte ausgewählt werden, die noch nicht existiert, und dann anschließen an einen Vektor gebunden wird. Die Referenz zum Vektorobjekt wird also über den Namen im Dataframe erzeugt.

df_lineup$Geburtsjahr <- DJ_Geburtsjahr
df_lineup
##      Name Alter DJ_Vinyl Geburtsjahr
## 1 DJ Puma    34    FALSE        1988
## 2 Cabanne    38     TRUE        1984
## 3   Molly    28     TRUE        1994
## 4 Echoton    25    FALSE        1997
## 5   cv313    20    FALSE        2002

4.5.3 Operationen auf Datentabellen

Die in einer Datentabelle gespeicherten Objekte können in Funktionsaufrufen verwendet werden.

mean(df_lineup$Alter)
## [1] 29

4.6 Prüfe dich selbst

4.7 Videos zum Kapitel

Homogene Strukturierte Datentypen (Vektor und Matrix)

Heterogene Strukturierte Datentypen (Liste und Dataframe)

4.8 Literaturverweise

Ergänzend

Weiterführend

Quellen

Grolemund, Garrett. 2014. Hands-on Programming with r: Write Your Own Functions and Simulations. " O’Reilly Media, Inc.". https://rstudio-education.github.io/hopr/.
R Core Team. 2022a. “An Introduction to R.” https://cran.r-project.org/doc/manuals/r-release/R-intro.html.
———. 2022b. “R Language Definition.” https://cran.r-project.org/doc/manuals/r-release/R-lang.html.
Wickham, Hadley. 2019. Advanced r. CRC press. https://adv-r.hadley.nz/.