Kapitel 3 Atomare Datentypen

Datentypen sind die Grundlage einer jeden Programmiersprache und daher für deren Verständnis unerlässlich. Sie dienen dazu, verschiedene Typen zu unterscheiden, wie etwa Zahlen von Buchstaben. Das ist besonders wichtig, da wir mit unterschiedlichen ‘Typen’ unterschiedliche Operationen ausführen bzw. nicht ausführen können. Zum Beispiel können wir mit Zahlen rechnen, mit Buchstaben hingegen nicht. Mit logischen Bedingungen können wir wiederum Wahrheitswerte ermitteln, mit Zahlenwerten hingegen nicht. Zu wissen, welche Eigenschaften die verschiedenen Datentypen haben und welche Operationen mit diesen möglich sind, hilft dabei, vielen potenziellen Fehlern vorzubeugen und daraus entstehende Frustration zu vermeiden.

Zunächst einmal wollen wir uns die atomaren Datentypen anschauen. Diese bilden die Grundlage aller folgenden Datenstrukturen.

Datentyp	Beschreibung	Beispiel
integer	ganze Zahlen	-2L
numeric	rationale Zahlen	5.2456
logical	logische Werte	TRUE
character	Zeichenfolge	“Mexico”
NA,NULL,NaN	unbestimmt, leer, undefiniert
Inf	unendlich

Die numerischen Datentypen integer und numeric ermöglichen die Repräsentation numerischer Informationen. Mit dem Datentyp logical können logische Informationen dargestellt werden. Um symbolische Informationen zu repräsentieren, verwenden wir den Datentyp character. Mit numerischen, logischen und symbolischen Informationen ist es bereits möglich, eine Vielzahl von Sachverhalten auszudrücken. Was dies sein kann, wollen wir uns im Folgenden ansehen.

3.1 Arithmetische Grundoperationen und Basisfunktionen

R beherrscht für alle Zahlendarstellungen die arithmetischen Grundoperationen und eignet sich daher hervorragend als Taschenrechner.

Operation	Beschreibung	Beispiel
+,-	Addition, Subtraktion	3-1.2
*,/	Multiplikation, Division	4.8/4
^	Potenz	5^2

Beispiel:

1+2

## [1] 3

2*3.5

## [1] 7

10.1^3

## [1] 1030.301

Zusätzlich verfügt R für Daten numerischen Typs über viele elementare Grundfunktionen. Hier nur ein paar wenige relevante Beispiele:

Operation	Beschreibung	Beispiel
sqrt()	Quadratwurzel	sqrt(9)
abs()	Absolutbetrag	abs(-12)
log(),exp()	Logarithmus und Expontentialfunktion	exp(3)
round()	Runden	round(2.12)

sqrt(5)

## [1] 2.236068

log(3)

## [1] 1.098612

3.1.1 Funktionsaufrufe

Funktionen sind ein wichtiger Teil von R und werden syntaktisch durch eine öffnende und eine schließende Klammer nach dem Schema funktion() gekennzeichnet. Wir haben gerade bereits eine Funktion ausgeführt, indem wir sqrt(9) aufgerufen haben. Ausführlich werden Funktionen noch im Kapitel 5 besprochen. Ein paar Grundlagen wollen sollen hier aber schon einmal einführen:

Funktionsaufrufe erfolgen in der Regel über das Schema

Funktionsname(Argument 1, Argument 2, ...)

Beispiel: Die Funktion

signif(x,digits)

rundet eine Zahl x auf digits signifikante Stellen.

1. Argumente haben zumeist einen festen Namen, sodass diesen eindeutig Werte zugewiesen werden können:

  signif(x = 12.3456, digits = 3)

## [1] 12.3

2. Alternativ können aufgrund der Position bzw. der Ordnung den Argumenten Werte zugewiesen werden:

  signif(12.3456, 3)

## [1] 12.3

3.1.2 Objekte, Funktionen und Referenzen

“To understand computations in R, two slogans are helpful: Everything that exists is an object. Everything that happens is a function call.” (John M. Chambers) ²

• Funktionen haben wir gerade kennengelernt, also kennen wir auch schon “Everything that happens”.
• Objekte haben wir auch schon durchgehend verwendet.

Geben wir etwa 3 oder "password" in die Konsole ein, wird ein entsprechendes Objekt im Speicher erzeugt.

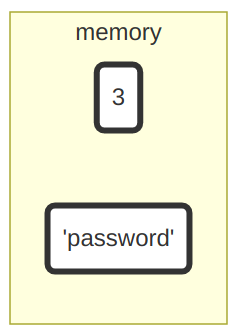
Auf diese Objekte haben wir allerdings anschließend keinen Zugriff mehr. Wenn wir zum Beispiel erneut die Zeichenkette "password" benötigten, müssten wir sie auch erneut eingeben. Wie wir das ändern können, damit uns die Objekte länger zur Verfügung stehen, wollen wir uns jetzt anschauen.

3.2 Erzeugung von referenzierbaren Objekten

Mit dem Operator <- lässt sich ein referenzierbares Objekt erstellen. Das bedeutet, dass das Objekt an einen Namen gebunden wird:

 x_test <- 3

Das Objekt lässt sich nun über den Namen aus dem Speicher abrufen:

x_test

## [1] 3

Wenn wir

 x_test <- 3

ausführen, passiert formal eigentlich Folgendes:

1. Es wird im Speicher ein Objekt mit dem Wert 3 erzeugt.
2. Der Name x_test wird an dieses Objekt gebunden, so dass auf das Objekt über den Namen x_test zugegriffen werden kann bzw. beim Aufruf von x_test der Wert zurückgegeben wird.

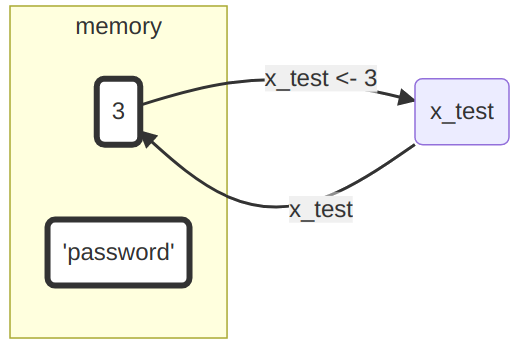
Über den Namen, welcher nun an das Objekt gebunden ist, können wir dieses jetzt dauerhaft abrufen (referenzieren).

3.2.1 Anmerkung Namen

Für Namen dürfen alle Buchstaben und Zahlen verwendet werden, sowie die beiden Sonderzeichen _ und ., wobei diese nichtam Anfang stehen dürfen.

Beispiel:

x_1 <- 3

Aber:

_x_1 <- 3

## Error: <text>:1:2: unexpected symbol
## 1: _x_1
##      ^

Bemerkung: Man sollte sich bei den Buchstaben nur auf a,…,z bzw. A,.., Z beschränken, auch wenn je nach lokalem Setting z.B. auch andere Buchstaben wie ä zulässig sind.

3.2.2 Rechnungen mit Werten von Objekten

Das über seinen Namen referenzierbare Objekt steht für alle weiteren Berechnungen und Operationen zur Verfügung:

x_test + 2

## [1] 5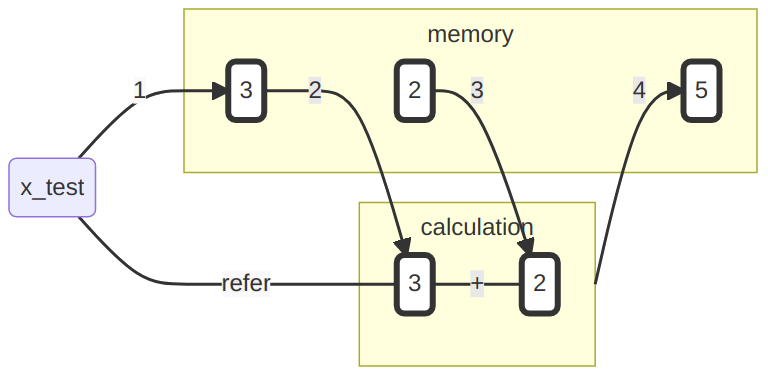

Das Ergebnis dieses Ausdrucks ist ein neues numerisches Objekt. Dieses kann für spätere Zwecke erneut an einen Namen gebunden werden:

y_test <- x_test + 2

y_test

## [1] 5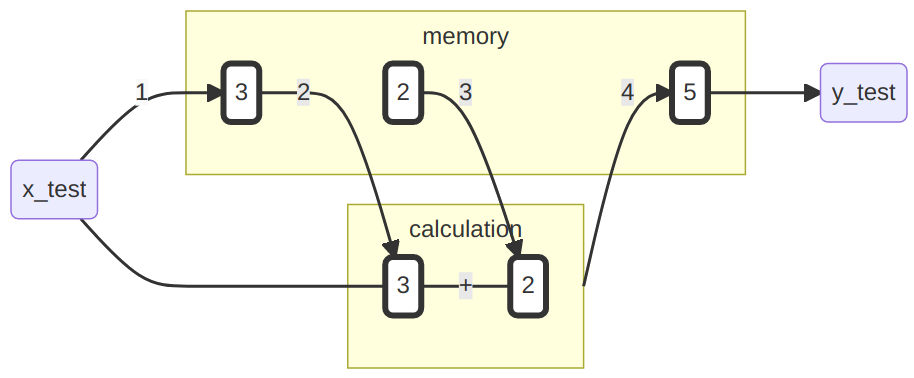

Unser Speicher sieht aktuell so aus:

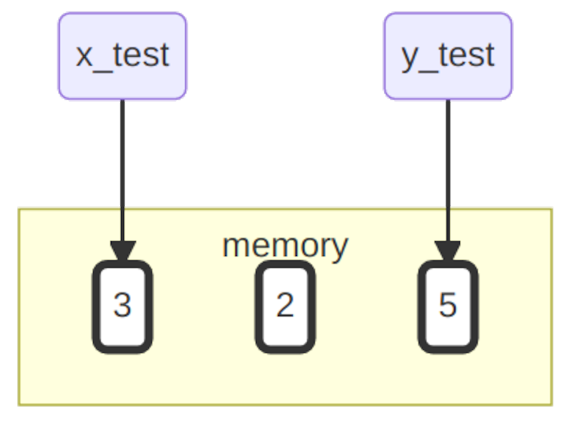
Zwar haben wir für die Berechnung auch eine Zwei im Speicher angelegt, diese ist aber nicht an einen Namen gebunden. Die Drei und die Fünf hingegen schon. Wenn wir nun x_test und y_test aufrufen, erhalten wir jeweils das entsprechende Objekt zurück.

3.2.3 Namen überschreiben

ACHTUNG! - Verwendet man denselben Namen noch einmal, geht die ursprüngliche Referenz verloren:

y_test <- log(y_test)

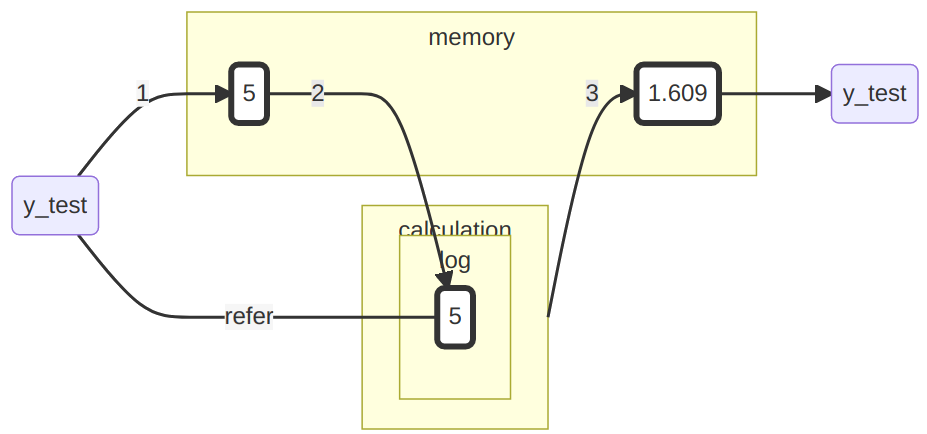
Wenn wir jetzt das Objekt zum Namen y_test abfragen, sehen wir Folgendes:

y_test

## [1] 1.609438

Das ursprüngliche Objekt zum Namen y_test steht uns nicht mehr zur Verfügung und ist somit unwiederbringlich verloren.

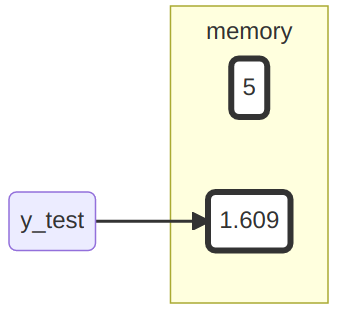
Führt man die Codezeile y_test <- log(y_test) jetzt noch einmal aus, so wird y_test wieder an ein anderes Objekt gebunden. Durch dieses Verhalten kann man nie mit Sicherheit vorhersagen, an welches Objekt y_test gerade gebunden ist. Aus diesem Grund sollte man immer neue Namen vergeben und diese nicht doppelt verwenden.

3.2.4 Objekte löschen

Wir haben mittlerweile ein paar Objekte im Speicher angelegt und an Namen gebunden. Mit ls() kann man diese abrufen:

ls()

##  [1] "D"                  "DJ_Alter"           "DJ_Geburtsjahr"    
##  [4] "DJ_Name"            "DJ_Vinyl"           "M"                 
##  [7] "X"                  "alter_moni"         "alter_tom"         
## [10] "base_plot"          "countdown"          "df_lineup"         
## [13] "df_regio"           "grades"             "i"                 
## [16] "is.positive"        "name"               "name_bundeskanzler"
## [19] "p"                  "pow"                "profil_marie"      
## [22] "q"                  "quadrat"            "starwars"          
## [25] "theendoftheworld"   "un_lambda"          "v1"                
## [28] "v1_log"             "v2"                 "x"                 
## [31] "x_1"                "x_test"             "y"                 
## [34] "y_test"             "z"                  "zahl"

Mit rm() kann man unnötige Objekte über deren Namen entfernen:

rm(y_test)

Wenn ihr gleich alle angelegten, referenzierbaren Objekte aus dem Speicher entfernen wollt:

rm(list = ls())

3.3 Logische Werte und Operationen

Die Werte Wahr und Falsch werden in R mit TRUE und FALSE repräsentiert. Es stehen die elementaren booleschen Operationen zur Verfügung.

Operator	Bedeutung
!	Negation
&	Und
|	Oder

p <- TRUE
!p

## [1] FALSE

q <- FALSE

(p | q)

## [1] TRUE

3.3.1 Der “logische” Wert NA

Neben Wahr und Falsch existiert noch die logische Konstante NA, welche für einen unbestimmten aber bestimmbaren Wert steht (not assigned, not available yet).

Dieser Wert wird z.B. universell für alle atomaren Datentypen für die Codierung von Fehlwerten (missings) verwendet.

theendoftheworld <- NA

3.3.2 Vergleichs-Operationen

Logische Werte spielen in R an verschiedenen Stellen eine Rolle, zum Beispiel als Rückgabewerte eines Vergleichs, ob dieser positiv ausgefallen ist oder nicht. Gänge Vergleichsoperatoren sind hier aufgelistet:

Operator	Bedeutung
==	Gleich?
!=	Ungleich?
> / <	Größer / Kleiner?
>= / <=	Größer / Kleiner gleich?

alter_tom <- 21
alter_moni <- 24
alter_tom > alter_moni

## [1] FALSE

3.4 Zeichenketten (character strings)

Neben Zahlen und logischen Werten werden wir auch Zeichenketten begegnen bzw. benötigen. Diese können auf zweierlei Art ausgezeichnet werden:

"Tom"

## [1] "Tom"

'Moni'

## [1] "Moni"

name_bundeskanzler <- "Olaf Scholz"
name_bundeskanzler

## [1] "Olaf Scholz"

3.5 Klasse eines Datenobjektes

Die Klasse bzw. was wir hier als Datentyp eines Objekts eingeführt haben lässt sich mit der Funktion class() ermitteln oder aber spezifisch/logisch prüfen.

class(alter_moni)

## [1] "numeric"

is.numeric(alter_moni)

## [1] TRUE

3.6 Spezielle Werte

Die leere Menge wird in R mit dem Wert NULL repräsentiert und dient ganz verschiedenen Zwecken wie z.B. der Initialisierung einer Variablen:

   z <- NULL
   z

## NULL

Division durch 0 ist “erlaubt” und liefert den speziellen Wert Inf zurück.

  100/0 

## [1] Inf

In R wird ein nicht bestimmbarer Wert (vgl. unbestimmter aber bestimmbarer Wert ‘NA’) durch NaN (not a number) angegeben.

3.7 Prüfe dich selbst

Von dieser Sitzung solltest du Folgendes mitgenommen haben:

• Du solltest verstanden haben, warum man verschiedene Datentypen unterscheidet.
• Du solltest die drei grundlegenden Wege in R Informationen zu repräsentieren kennen, und die dazugehörigen Datentypen nennen können.
• Du solltest verstanden haben, wie man Objekte an einen Namen bindet und warum das nützlich sein kann.
• Du solltest die elementaren Booleschen (logischen) Operationen in R schreiben können.

3.8 Videos zum Kapitel

3.8.1 Atomare Datentypen

3.8.2 Objektzuweisungen

3.9 Literaturverweise

Ergänzend

• R-Intro Kapitel 1 & 2
• Hands-On Programming with R Kapitel 2 (Ohne 2.4 & 2.5)

Weiterführend

• Advanced R Kapitel 2 und 12

Chambers (2014) Wickham (2019) R Core Team (2022a) Grolemund (2014)

Quellen

Chambers, John M. 2014. “Object-Oriented Programming, Functional Programming and r.” https://doi.org/10.48550/ARXIV.1409.3531.

Grolemund, Garrett. 2014. Hands-on Programming with r: Write Your Own Functions and Simulations. " O’Reilly Media, Inc.". https://rstudio-education.github.io/hopr/.

R Core Team. 2022a. “An Introduction to R.” https://cran.r-project.org/doc/manuals/r-release/R-intro.html.

Wickham, Hadley. 2019. Advanced r. CRC press. https://adv-r.hadley.nz/.

---

2. https://de.wikipedia.org/wiki/R_%28Programmiersprache%29↩︎